Separate a 2 person mixture

Separate a 2 person mixture by ranking the possible contributor pairs.

rank_contributor_pairs(contrib_pairs, fit, max_rank = NULL)

Arguments

contrib_pairs: A contrib_pairs object obtained from contributor_pairs.
fit: A disclapmixfit object.
max_rank: Not used. Reserved for future use.

Value

A ranked_contrib_pairs object that is basically an order vector and the probabilities for each pair (in the same order as given in contrib_pairs), found by using fit. Note, that contributor order is disregarded so that each contributor pair is only present once (and not twice as would be the case if taking order into consideration).

Examples


data(danes)
db <- as.matrix(danes[rep(1L:nrow(danes), danes$n), 1L:(ncol(danes) - 1L)])

set.seed(1)
true_contribs <- sample(1L:nrow(db), 2L)
h1 <- db[true_contribs[1L], ]
h2 <- db[true_contribs[2L], ]
db_ref <- db[-true_contribs, ]

h1h2 <- c(paste(h1, collapse = ";"), paste(h2, collapse = ";"))
tab_db <- table(apply(db, 1, paste, collapse = ";"))
tab_db_ref <- table(apply(db_ref, 1, paste, collapse = ";"))
tab_db[h1h2]
#> 
#> 14;12;28;22;10;11;13;16;10;11 16;13;30;25;10;11;13;14;11;10 
#>                             9                             1 
tab_db_ref[h1h2]
#> 
#> 14;12;28;22;10;11;13;16;10;11                          <NA> 
#>                             8                               

rm(db) # To avoid use by accident

mixture <- generate_mixture(list(h1, h2))

possible_contributors <- contributor_pairs(mixture)
possible_contributors
#> Mixture:
#>   DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> 1 14,16   12,13    28,30  22,25     10     11     13  14,16  10,11  10,11
#> 
#> Number of possible contributor pairs = 64

fits <- lapply(1L:5L, function(clus) disclapmix(db_ref, clusters = clus))

best_fit_BIC <- fits[[which.min(sapply(fits, function(fit) fit$BIC_marginal))]]
best_fit_BIC
#> disclapmixfit from 183 observations on 10 loci with 4 clusters.
#> 
#> EM converged:                                                       TRUE
#> Number of central haplotype changes:                                0
#> Total number of EM iterations:                                      16
#> Model observations (n*loci*clusters):                               1830
#> Model parameters ((clusters*loci)+(loci+clusters-1)+(clusters-1)):  56
#> GLM method:                                                         internal_coef
#> Initial central haplotypes supplied:                                FALSE
#> Method to find initial central haplotypes:                          pam

ranked_contributors_BIC <- rank_contributor_pairs(possible_contributors, best_fit_BIC)
ranked_contributors_BIC
#> Mixture:
#>   DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> 1 14,16   12,13    28,30  22,25     10     11     13  14,16  10,11  10,11
#> 
#> Contributor pairs = 64
#> 
#> Sum of all (product of contributor pair haplotypes) = 2.375477e-05
#> 
#> Showing rank 1-5:
#> 
#> Rank 1 [ P(H1)*P(H2) = 1.384459e-05 ]:
#>    DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> H1    14      12       28     22      .      .      .     16     10     11
#> H2    16      13       30     25      .      .      .     14     11     10
#>           Prob
#> H1 0.042522055
#> H2 0.000325586
#> 
#> Rank 2 [ P(H1)*P(H2) = 9.155864e-06 ]:
#>    DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> H1    14      12       28     22      .      .      .     16     10     10
#> H2    16      13       30     25      .      .      .     14     11     11
#>           Prob
#> H1 0.006408721
#> H2 0.001428657
#> 
#> Rank 3 [ P(H1)*P(H2) = 2.128967e-07 ]:
#>    DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> H1    14      13       30     25      .      .      .     14     11     10
#> H2    16      12       28     22      .      .      .     16     10     11
#>            Prob
#> H1 0.0003255861
#> H2 0.0006538875
#> 
#> Rank 4 [ P(H1)*P(H2) = 1.67922e-07 ]:
#>    DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> H1    14      13       28     22      .      .      .     16     10     11
#> H2    16      12       30     25      .      .      .     14     11     10
#>            Prob
#> H1 3.808357e-03
#> H2 4.409302e-05
#> 
#> Rank 5 [ P(H1)*P(H2) = 1.407953e-07 ]:
#>    DYS19 DYS389I DYS389II DYS390 DYS391 DYS392 DYS393 DYS437 DYS438 DYS439
#> H1    14      13       30     25      .      .      .     14     11     11
#> H2    16      12       28     22      .      .      .     16     10     10
#>            Prob
#> H1 1.428657e-03
#> H2 9.855081e-05
#> 
#>  (59 contributor pairs hidden.)

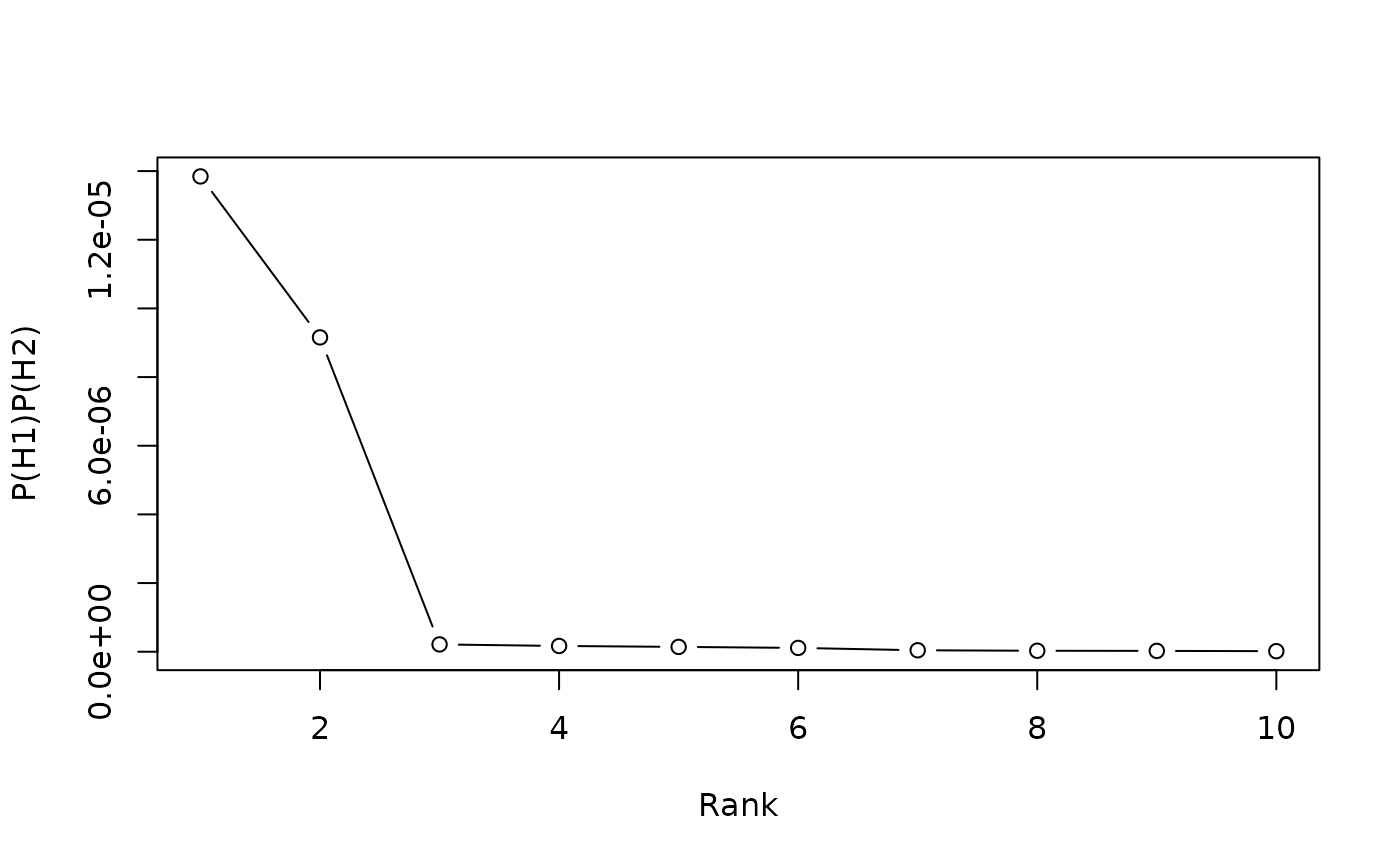
plot(ranked_contributors_BIC, top = 10L, type = "b")


get_rank(ranked_contributors_BIC, h1)
#> [1] 1

Arguments

Value

See also

Examples