Estimate error probability, w, using a Bayesian approach

A Beta prior is assumed. Note that $w$ is assumed to be $< 0.5$.

Usage

estimate_w_bayesian(
  x,
  prior_a = 1,
  prior_b = 1,
  chains = 4,
  chains_function = lapply,
  warmup = 1000,
  iterations = 10000,
  ...
)

Arguments

x: either a 3x3 contingency table or 3-vector with counts (n1, n2, n3) where n1 = sum(diag(x)), n2 = x[1L, 3L] + x[3L, 1L], n3 = sum(x) - n1 - n2
prior_a: First shape parameter for prior beta distribution
prior_b: Second shape parameter for prior beta distribution
iterations: Number of iterations
...: Not used

Details

NOTE: We recommend using e.g. the cmdstanr, see the vignette. This is just an implementation that demonstrate the Bayesian approach.

Examples

tab1 <- matrix(c(1000, 10, 2, 12, 100, 8, 1, 7, 200), nrow = 3)
tab1
#>      [,1] [,2] [,3]
#> [1,] 1000   12    1
#> [2,]   10  100    7
#> [3,]    2    8  200
estimate_w(tab1)
#> [1] 0.008154441
y <- estimate_w_bayesian(tab1)
q <- posterior_samples(y)
mean(q); #plot(q, type = "l"); hist(q)
#> [1] 0.008408054
sapply(y, \(x) x$acceptance_ratio)
#> [1] 0.2224 0.2187 0.2124 0.2229

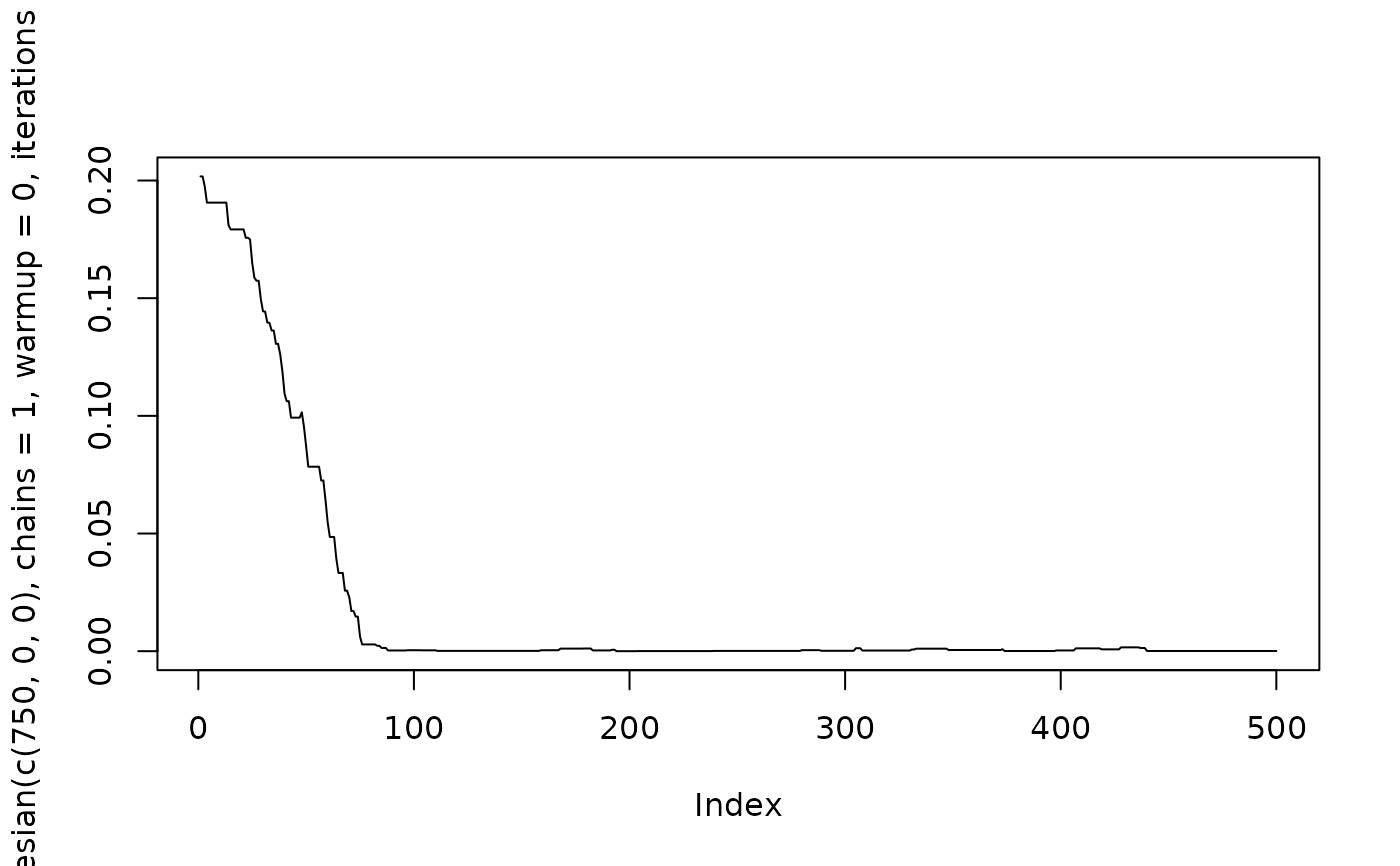
estimate_w_bayesian(c(750, 0, 0), chains = 1, warmup = 0, iterations = 500) |> 
   lapply(\(x) x$samples) |> unlist() |> plot(type = "l")


estimate_w(c(750, 0, 0))
#> [1] 9.733533e-17
y <- estimate_w_bayesian(c(750, 0, 0)); q <- lapply(y, \(x) x$samples) |> unlist()
mean(q); #plot(q, type = "l"); hist(q)
#> [1] 0.0003386582
sapply(y, \(x) x$acceptance_ratio)
#> [1] 0.0624 0.0645 0.0666 0.0634