Skip to contents

Error rate uncertainty

Source: vignettes/error-rate-uncertainty.Rmd
error-rate-uncertainty.Rmd
q1 <- 0.4
p1 <- c(q1^2, 2*q1*(1-q1), (1-q1)^2)
sum(p1)
#> [1] 1
q2 <- 0.3
p2 <- c(q2^2, 2*q2*(1-q2), (1-q2)^2)
sum(p2)
#> [1] 1
# t: trace sample
# r: reference sample
LRs <- calc_LRs_wTwR(xT = c(0, 0), xR = c(0, 0), wT = 1e-2, wR = 1e-6, p = list(p1, p2))
WoE <- sum(log10(LRs))
WoE
#> [1] 1.808338
shppars <- get_beta_parameters(mu = 1e-2, sigmasq = 1e-3)
shppars
#> [1] 0.078 3.822
curve(dbeta05(x, shppars[1], shppars[2]), from = 0, to = 0.5)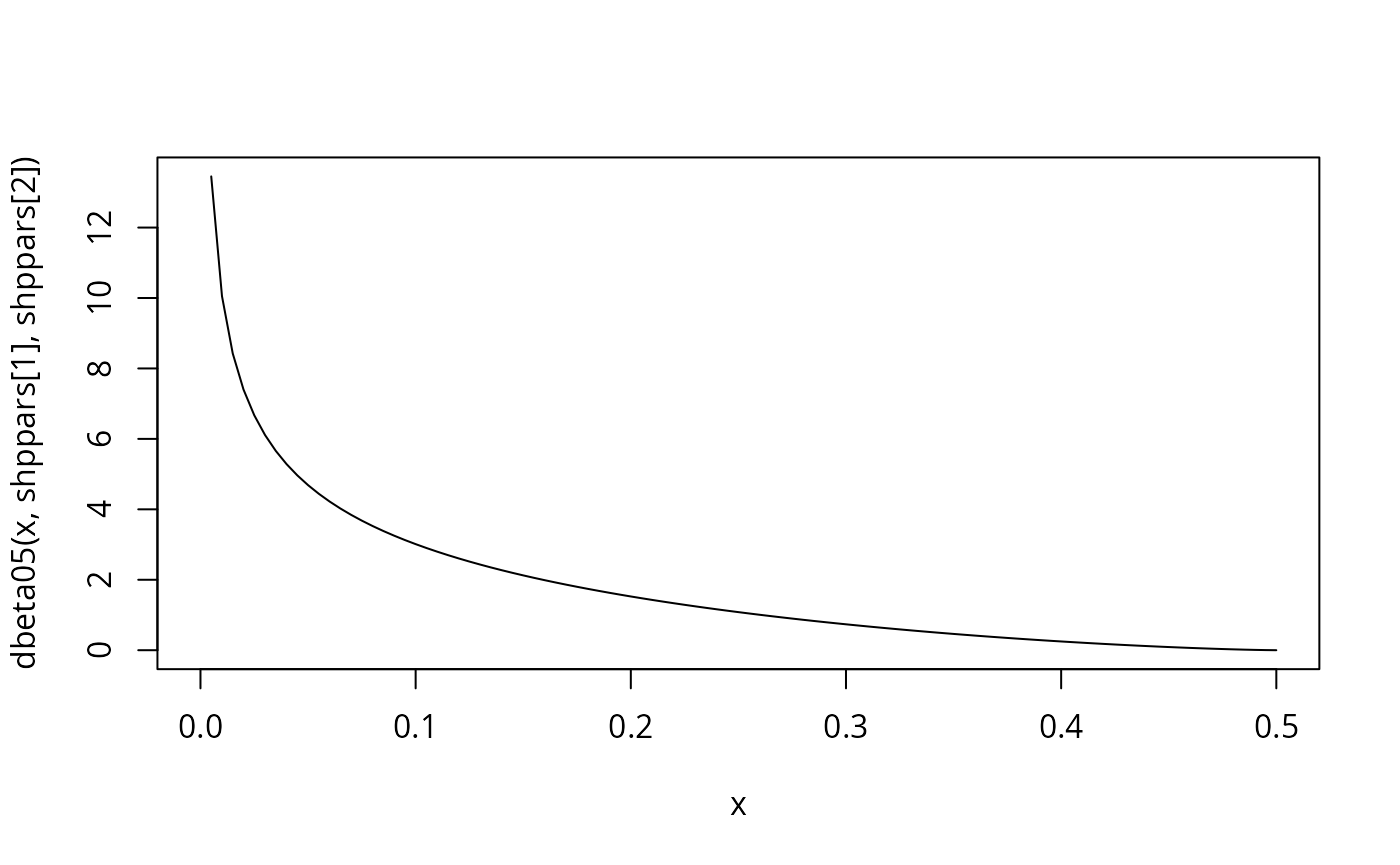

z1 <- calc_WoE_wTwR_integrate_wT_mc(xT = c(0, 0), xR = c(0, 0), 
                                    wR = 1e-6, 
                                    shape1T = shppars[1],
                                    shape2T = shppars[2],
                                    p = list(p1, p2))
z1$WoE
#> [1] 1.810701
z2 <- calc_WoE_wTwR_integrate_wT_num(xT = c(0, 0), xR = c(0, 0), 
                                     wR = 1e-6, 
                                     shape1T = shppars[1],
                                     shape2T = shppars[2],
                                     p = list(p1, p2))
z2$WoE
#> [1] 1.808099

And markerwise (integrating at each marker), does not necessarily give same results as the expected value of the WoE (as calculated above):

WoEs_mc <- calc_WoE_wTwR_integrate_wT_mc_markerwise(
  xT = c(0, 0), xR = c(0, 0), 
  wR = 1e-6, 
  shape1T_H1 = shppars[1], shape2T_H1 = shppars[2],
  shape1T_H2 = shppars[1], shape2T_H2 = shppars[2],
  p = list(p1, p2),
  n_samples = 10000)
WoEs_mc
#> [1] 0.7823008 1.0256404
sum(WoEs_mc)
#> [1] 1.807941
z1$WoEs
#> [1] 0.7834855 1.0272160

WoEs_exact <- calc_WoE_wTwR_integrate_wT_exact_markerwise(
  xT = c(0, 0), xR = c(0, 0), 
  wR = 1e-6, 
  shape1T_H1 = shppars[1], shape2T_H1 = shppars[2],
  shape1T_H2 = shppars[1], shape2T_H2 = shppars[2],
  p = list(p1, p2))
WoEs_exact
#> [1] 0.7831524 1.0252129
sum(WoEs_exact)
#> [1] 1.808365
z1$WoEs
#> [1] 0.7834855 1.0272160

Profile likelihood (maximising under each hypothesis), assuming same genotyping error probability for all markers:

x <- calc_WoE_wTwR_profilemax_wT_num(
  xT = c(0, 0),
  xR = c(0, 0),
  wR = 1e-6,
  p = list(p1, p2))
x$WoE
#> [1] 1.204115
x$wT_H1
#> [1] 1e-06
x$wT_H2
#> [1] 0.5
10^x$log10PrE_H1
#> [1] 0.01439988
10^x$log10PrE_H2
#> [1] 0.0009000033